Elsewhere, Pierre Lemieux asked In two sentences, what do you think of the Monty Hall paradox?
Unless I construct sentences loaded with conjunctions (which would seem to violate the spirit of the request), an answer in just two sentences will be unsatisfactory (though I provided one). Here in my 'blog, I'll write at greater length.
The first appearance in print of what's called the Monty Hall Problem
seems to have been in a letter by Steve Selvin to The American Statistician v29 (1975) #1. The problem resembles those with which Monty Hall used to present contestants on Let's Make a Deal, though Hall has asserted that no problem quite like it were presented on that show. The most popular statement of the Monty Hall Problem came in a letter by Craig Whitaker to the Ask Marilyn
column of Parade:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, Do you want to pick door No. 2?
Is it to your advantage to switch your choice?
(Before we continue, take car
and goat
to stand, respectively, for something that you want and something that you don't want, regardless of your actual feelings about cars and about goats.)
There has been considerable controversy about the proper answer, but the text-book answer is that, indeed, one should switch choices. The argument is that, initially, one has a 1/3 probability that the chosen Door has the car, and a 2/3 probability that the car is behind one of the other two Doors. When the host opens one of the other two Doors, the probability remains that the car is behind one of the unchosen Doors, but has gone to 0 for the opened Door, which is to say that the probability is now 2/3 that the car is behind the unchosen, unopened Door.
My first issue with the text-book answer is with its assignment of initial, quantified probabilities. I cannot even see a basis for qualitative probabilities here; which is to say that I don't see a proper reason for thinking either that the probability of the car being behind a given Door is equal to that for any other Door or that the probability of the car being behind some one Door is greater than that of any other Door. As far as I'm concerned, there is no ordering at all.
The belief that there must be an ordering usually follows upon the even bolder presumption that there must be a quantification. Because quantification has proven to be extremely successful in a great many applications, some people make the inference that it can be successfully applied to any and every question. Others, a bit less rash, take the position that it can be applied everywhere except where it is clearly shown not to be applicable. But even the less rash dogma violates Ockham's razor. Some believe that they have a direct apprehension of such quantification. However, for most of human history, if people thought that they had such literal intuitions then they were silent about it; a quantified notion of probability did not begin to take hold until the second half of the Seventeenth Century. And appeals to the authority of one's intuition should carry little if any weight.
Various thinkers have adopted what is sometimes called the principle of indifference
or the principle of insufficient reason
to argue that, in the absence of any evidence to the contrary, each of n collectively exhaustive and mutually exclusive possibilities must be assigned equal likelihood. But our division of possibilities into n cases, rather than some other number of cases, is an artefact of taxonomy. Perhaps one or more of the Doors is red and the remainder blue; our first division could then be between two possibilities, so that (under the principle of indifference) one Door would have an initial probability of 1/2 and each of the other two would have a probability of 1/4.
Other persons will propose that we have watched the game played many times, and observed that a car has with very nearly equal frequency appeared behind each of the three Doors. But, while that information might be helpful were we to play many times, I'm not aware of any real justification for treating frequencies as decision-theoretic weights in application to isolated events. You won't be on Monty's show to-morrow.
Indeed, if a guest player truly thought that the Doors initially represented equal expectations, then that player would be unable to choose amongst them, or even to delegate the choice (as the delegation has an expectation equal to that of each Door); indifference is a strange, limiting case. However, indecision — the aforementioned lack of ordering — allows the guest player to delegate the decision. So, either the Door was picked for the guest player (rather than by the guest player), or the guest player associated the chosen Door with a greater probability than either unchosen Door. That point might seem a mere quibble, but declaring that the guest player picked the Door is part of a rhetorical structure that surreptitiously and fallaciously commits the guest player to a positive judgment of prior probability. If there is no case for such commitment, then the paradox collapses.
Well, okay now, let's just beg the question, and say not only that you were assigned Door Number 1, but that for some mysterious reason you know that there is an equal probability of the car being behind each of the Doors. The host then opens Door Number 3, and there's a goat. The problem as stated does not explain why the host opened Door Number 3. The classical statement of the problem does not tell the reader what rule is being used by the host; the presentation tells us that the host knows what's behind the doors
, but says nothing about whether or how he uses that knowledge. Hypothetically, he might always open a Door with a goat, or he might use some other rule, so that there were a possibility that he would open the Door with a car, leaving the guest player to select between two concealed goats.
Nowhere in the statement of the problem are we told that you are the sole guest player. Something seems to go very wrong with the text-book answer if you are not. Imagine that there are many guest players, and that outcomes are duplicated in cases in which more than one guest player selects or is otherwise assigned the same Door. The host opens Door Number 3, and each of the guest players who were assigned that Door trudges away with a goat. As with the scenario in which only one guest player is imagined, more than one rule may govern this choice made by the host. Now, each guest player who was assigned Door Number 1 is permitted to change his or her assignment to Door Number 2, and each guest player who was assigned Door Number 2 is allowed to change his or her assignment to Door Number 1. (Some of you might recall that I proposed a scenario essentially of this sort in a 'blog entry for 1 April 2009.) Their situations appear to be symmetric, such that if one set of guest players should switch then so should the other; yet if one Door is the better choice for one group then it seems that it ought also to be the better for the other group.
The resolution is in understanding that the text-book solution silently assumed that the host were following a particular rule of selection, and that this rule were known to the guest player, whose up-dating of probabilities thus could be informed by that knowledge. But, in order for the text-book solution to be correct, all players must be targeted in the same manner by the response of the host. When there is only one guest player, it is possible for the host to observe rules that respond to all guest players in ways that are not not possible when there are multiple guest players, unless they are somehow all assigned the same Door. It isn't even possible to do this for two sets of players each assigned different Doors.
Given the typical presentation of the problem, the typical statement of ostensible solution is wrong; it doesn't solve the problem that was given, and doesn't identify the problem that was actually solved.
[No goats were harmed in the writing of this entry.]

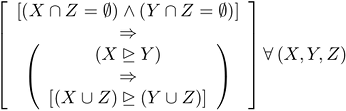 in which X, Y, and Z are sets of events. The underscored arrowhead is again my notation for
in which X, Y, and Z are sets of events. The underscored arrowhead is again my notation for 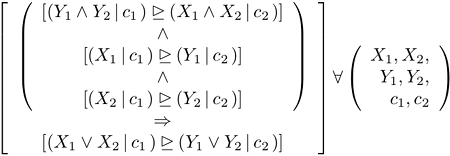 To get di Finetti's principle from it, set
To get di Finetti's principle from it, set 

