I believe that violence will erupt amongst those tasked with counting the votes and with overseeing that counting, for the upcoming General Election. More specifically, I expect that Democrats will attempt forceably to exclude Republicans in these tasks, that Republicans will respond with counter-force, and that the mainstream of the media will present the fighting as caused by the Republicans.

I began predicting such behavior weeks ago, but I have not previously posted the prediction here.

The axiom of Generalized Decomposition from Formal Qualitative Probability may be refactored to This refactoring is mathematically trivial, exploiting two automorphisms, but exhibits the principle more elegantly.

The axiom of Disjunctive Presumption in Formal Qualitative Probability may be more simply stated as

Measures — quantities to which some arithmetic can be meaningfully applied — can be fitted to some human attributes, even if not to others. When attempting to compare some populations to others, an assumption is made that the properties of the individuals within these populations are subject to quantification of some sort, and that the quantities are commensurable across populations. But usually these assumptions are implicit and unrecognized, and even those who have some awareness that they are dealing with quantities very often don't have a proper grasp of elementary issues.

Very often, people try to understand distinct populations in terms of some notion of averages. If each and every member of every population were exactly average in every regard, then averages would be perfect measures of the populations as such. More generally, if for any two populations the share of that population deviating from average by some specific amount were the same, averages would be sufficient for any comparison of the attributes of populations, except for population sizes. But if the overall variance from average in one population is different from that in another, then thinking in terms of averages can go very, very wrong.

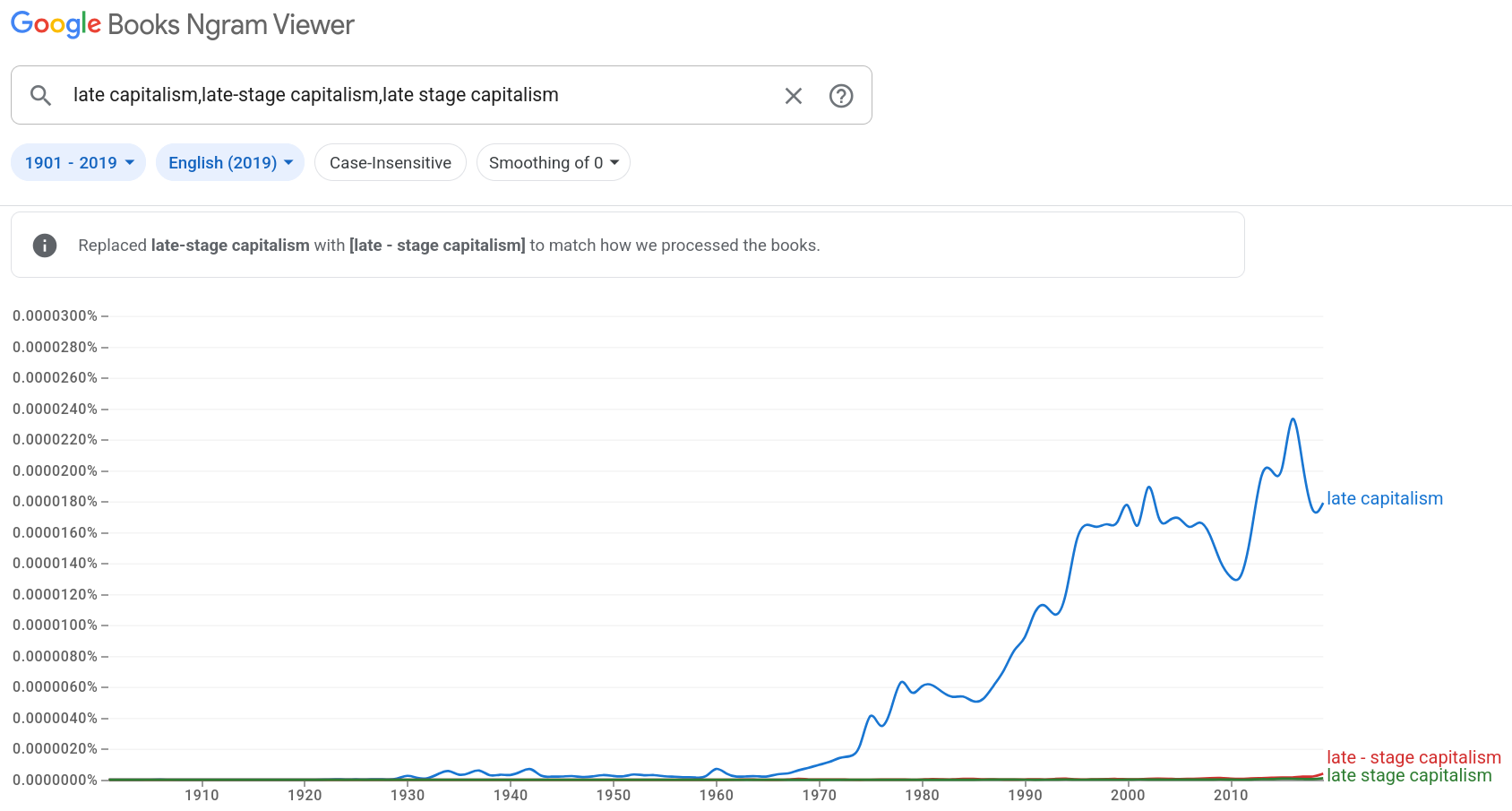
Here are hypothetic distributions for some attribute within two populations, each population having the same number of members:[1] For both Population A and Population B, the median[2] of the attribute is the same, but Population B has more variance from the arithmetic mean than does Population A. Even though each of these two populations have the same median, more members of the population of greater variance are below some some measure, and more members of that same population are above some measure. Population B₂ has the same variance as Population B, but the same arithmetic mean (rather than median) as Population A. Again, even though the center is, by some measure, the same for both populations, more members of the population of greater variance are below some some measure, and more members of that same population are above some measure.

Even if a population has a higher center than Population A, if it has a greater variance then it will dominate the lower range of measures below some measure. And even if a population has a lower center than Population A, if it has a greater variance then it will dominate the higher range of measures beyond some measure.

If a measurable attribute correlates positively with social success, then ceteris paribus, a population of higher variance is going to dominate both social winners beyond some level and social losers below some level. If a population generally has greater variance amongst its attributes, then — discarding the assumption of ceteris paribus — that population is going to dominate both social winners beyond some level and social losers below some level; even if it has the same median or same mean or even a lower center than another populations.

In fact, though I cannot readily graph the cases in which attributes are only partially ordered and not measurable, the reader should see that the underlying point does not depend upon the measurability of the attributes, but only upon one population having greater propensity for variance than another.

But

• If one is only looking at the losers and thoughtlessly assuming that their numbers are explained by averages, then one is going inappropriately to infer that the population is generically inferior.
• If one is only looking at the losers, while thoughtlessly assuming that the averages are the same and that nothing else about the population itself can explain the difference in outcomes, then one is going inappropriately to infer that the population are victims of systemic bias.
• If one is only looking at the winners and thoughtlessly assuming that their numbers are explained by averages, then one is going inappropriately to infer that the population is generically superior.
• If one is only looking at the winners, while thoughtlessly assuming that the averages are the same and that nothing else about the population itself can explain the difference in outcomes, then one is going inappropriately to infer that any rival population are victims of systemic bias.

In each case, if we look at the other end of the distribution, the thoughtless conclusion falls apart.

When the last of these errors is made, an attempt may be undertaken to offset illusory bias, by putting an institutional thumb on the scales to shift Population A generally forward, until the the number of social winners at every level is at least the same. But notice what is then really happening 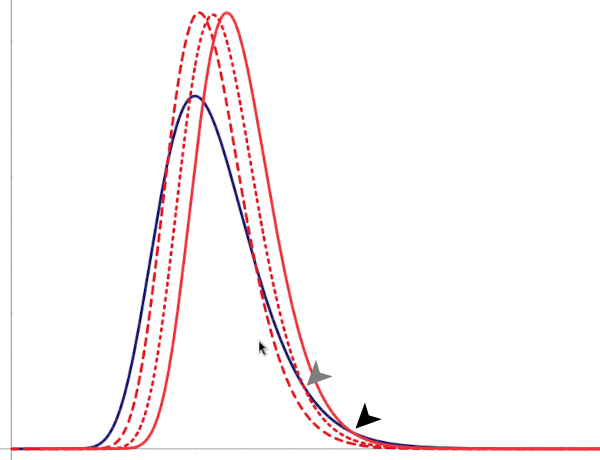as the relative outcomes for most members of the population of greater variance fall increasingly below those of the population of less variance — at previously targetted levels the population of lower variance comes to enjoy greater social success than does the population of greater variance. And notice that the population of greater variance necessarily still dominates above some value, albeït that the value increases as the institutional thumb comes down ever harder in a misguided attempt to match the upper tails of the distribution.

Only actual systemic bias can bring the number of social winners across populations into equality above any given level of social success beyond the center; and, the larger the population, the greater the required bias for such an outcome, and the more that most of the population of greater variance are victimized.

If the two populations are not equal in size, then the foregoing analysis would simply need to entail talk of proportionality. But one might as well speak and write of two populations of the same size, because the real-world application involves two populations that are very close to the same size in most first-world nations. The greater variance of one of those two populations is a consequence of the greater chaos in the formation of one of that population's chromosomes and of a lack of redunancy for another.

Unfortunately, most of the attempts to analyze what has been happening has entailed ham-fisted theorizing about differing averages.

[1] A population with finite membership cannot perfectly conform to a continuous distribution function; but, the larger the population, the less the necessary non-conformance.

[2] The median for each population is the point such that as many members of the population are above it as are below it.

Often, when talking about the distribution of measurable human attributes, people refer to the bell curve, which is to say to a Gaussian distribution, more commonly known as a normal distribution.

One immediate difficulty is that the Gaussian distribution extends symmetrically without lower limit to measurements with positive probability, whereas the natural measures of most of the attributes that will interest us have lower limits of possibility (typically at or above zero). For example, no one has negative weight or negative height. Simply truncating the lower bound of a Gaussian distribution usually doesn't make a great deal of sense, because few people will even be near the lower bound, rather than a fair number at it or just barely above it.

Instead, the distribution will more typically look something like this:

Mind you that measures can always be transformed, and a measure that has a lower bound of b can be transformed into a measure without lower bound simply by the device of subtracting the bound and then taking a logarithm: measure₁(x) = log_e[measure₀(x) - b] Some set of transformations can surely be used to arrive at one with a distribution that is well approximated by a Gaussian distribution. But, for the most part, I'd rather use natural or familiar measures than manipulate the data to arrive at a Gaussian distribution, especially as one otherwise typically needs to invert the transformations at the end of the analysis, to make sense of things.

In the near future, I plan to post an entry about misreading the consequences of different variances in different human populations. What I have to say could all be expressed in terms of Gaussian distributions, but I don't want to do so, nor did I want that future entry to begin with a discussion such as that here.

The immoderate political left began speaking and writing of late[-stage] capitalism with the end of the First World War.

The idea has been that the industrialized world has entered the final stage of something called capitalism, with a revolutionary change to some form of socialism just around the corner…

…for more than a century now.

(Actually what we've seen is a slow, grinding transformation away from the use of genuine markets to an administrated order, which in more recent years has threatened to become a neo-feudalism. The transformation began well before the First World War, as technocratic thinking began displacing liberalism.)

To-day, I updated some software on a Samsung electronic tablet. The latest version comes with an ability to suggest changes on-the-fly to what I've written. These changes include to wording that Samsung calls Professional, to what they call Casual, or to what they call Social. What they call Social seems to be what they call Casual, with the addition of hashtags. What they call Professional certainly isn't very professional.

The software may already have been patched to address this specific error, but I'm sure that many other errors remain, and they will propagate. For decades now, a great many people, even people who imagine themselves as native speakers of the English language, have been uncritically accepting what software has told them about the language.

I will sometimes use software to check my spelling, but I don't simply make every change that it suggests. I find that, in analyzing my writing, grammar-checkers so often flag constructions that are actually correct and so seldom find real errors that these checkers are not worth running. And a person who relies upon software for tone is falsifying his or her relationships.

I still await a first decision from the journal to which on 24 February I submitted my paper on Sraffa. On 27 May, I queried the editor about when I might expect a decision. My query was really to ensure that the paper weren't mislaid; I've more than one unfortunate experience of such a thing. On 29 May, I received a reasonable and polite response that he hoped to have a report from the reviewer within a month.

The mission statement of the journal from which I yanked that paper on 21 February declares

Our goal is to provide a definitive answer within one month of submission.

I yanked the paper, submitted on 23 January, after it had idled for four weeks without being sent to the editor-in-chief. On 28 March they none-the-less reported it as placed in the hands of the editor-in-chief.

When I'd yanked the paper, when I received this notice, and when I received an apology and plea for patience, I sent copies of my replies (declaring and reïterating that the paper were no longer on-offer to them) to that editor-in-chief. None-the-less, on 07 June — more than four months after my submission — the editor sent a rejection on the grounds that the work were primarily exegetic. I think that the behavior of the editor and of the administrative staff betrays a gross disorganization that makes a mockery of the supposèd goal of reaching a decision within a month.

Imagining all of a society's various generation and allocation of goods and services as if the creation and distribution of one big pie is very much analogous to imagining all of the sexual interactions of that society as one enormous orgy.

I have not voted for any Presidential candidate since the 1988 General Election, and I will not be voting for any Presidential candidate in the 2024 General Election.

As I and very many people before me have noted, my vote or non-vote in any present election of significance has no effect on the outcome that election. The margin by which any candidate in such an election wins or loses is always in the thousands of vote, so that an individual vote could be given to a different candidate or simply not cast, without a different winner resulting. But, as I have also noted, a vote cast or withheld in a present election has some effect, albeït usually very small, on the subsequent behavior of those active in the political process, as they have a sense of what they can't, can, or must do to win the next election, based upon the margins of victory and votes altogether withheld.

The least effective thing that a potential voter can do is to vote for a candidate whom he or she dislikes.

[…]

The most effective thing that a potential voter as such can do is to vote for a candidate of whom that voter approves, even if that candidate has no chance of winning, or to submit a ballot from which no candidate receives a vote.

I endorse submitting a ballot in which no Presidential candidate is selected. Where not given a better option to reject all candidates explicitly, a voter should enter something such as [ALL CANDIDATES REJECTED!] as-if a write-in vote, to prevent a poll-worker or election official otherwise taking advantage of the opportunity to check a box for his or her preferred candidate.

In the General Elections after 1988 and through 2020, I considered the Presidential nominees of the Libertarian Party, but rejected each. When, in 2020, Jo Jorgensen joined the pile on top of those who lost their jobs for saying all lives matter, I decided that I would not vote for any subsequent Presidential nominee of that party unless he or she unequivocally denounced Jorgensen and this later nominee's campaign acted to make Jorgensen's victims whole. Of course, I considered the chances of a nominee's taking such responsibility to be negligible.

Then, in August of 2021, Rebecca Lau, Chairman of the Manhattan Libertarian Party from 18 June 2021 to 10 October 2023, wrote My opinion is that the unvaccinated should die. This declaration began a cascade of fifteen-minute problems, with the Manhattan Libertarian Party, then the New York Libertarian Party, then the Libertarian Party National Committee, and finally all the remaining parties affilitated with the LPNC not effecting solutions. I consequently vowed never again to vote for any candidate of these parties for any office.