Years ago, I planned to write a paper on decision-making under uncertainty when possible outcomes were completely ordered neither by desirability nor by plausibility.
On the way to writing that paper, I was impressed by Mark Machina with the need for a paper that would explain how an incompleteness of preferences would operationalize, so I wrote that article before exploring the logic of the dual incompleteness that interested me.
Returning to the previously planned paper, I did not find existing work on qualitative probability that was adequate to my purposes, so I began trying to formulating just that as a part of the paper, and found that the work was growing large and cumbersome. I have enough trouble getting my hyper-modernistic work read without delivering it in large quantities! So I began developing a paper concerned only with qualitative probability as such.
In the course of writing that spin-off paper, I noticed that a rather well-established proposition concerning the axiomata of probability contains an unnecessary restriction; and that, over the course of more than 80 years, the proposition has repeatedly been discussed without the excessiveness of the restriction being noted. Yet it's one of those points that will be taken as obvious once it has been made. I originally planned to note that dispensibility in the paper on qualitative probability, but I have to be concerned about increasing clutter in that paper. Yester-day, I decided to write a note — a very brief paper — that draws attention to the needlessness of the restriction. The note didn't take very long to write; I spent more time with the process of submission than with that of writing.
So, yes, a spin-off of a spin-off; but at least it is spun-off, instead of being one more thing pending. Meanwhile, as well as there now being three papers developed or being developed prior to that originally planned, I long ago saw that the original paper ought to have at least two sequels. If I complete the whole project, what was to be one paper will have become at least six.
The note has been submitted to a journal of logic, rather than of economics; likewise, I plan to submit the paper on qualitative probability to such a journal. While economics draws upon theories of probability, work that does not itself go beyond such theories would not typically be seen as economics. The body of the note just submitted is only about a hundred words and three formulæ. On top of the usual reasons for not knowing whether a paper will be accepted, a problem in this case is exactly that the point made by the paper will seem obvious, in spite of being repeatedly overlooked.
As to the remainder of the paper on qualitative probability, I'm working to get its axiomata into a presentable state. At present, it has more of them than I'd like.
![[image of mathematic formula]](wp-content/uploads/2024/09/AP11.png) This refactoring is mathematically trivial, exploiting two automorphisms, but exhibits the principle more elegantly.
This refactoring is mathematically trivial, exploiting two automorphisms, but exhibits the principle more elegantly.

![[image of mathematic formula]](wp-content/uploads/2024/08/A9.png) may be more simply stated as
may be more simply stated as ![[image of mathematic formula]](wp-content/uploads/2024/08/AP7.png)
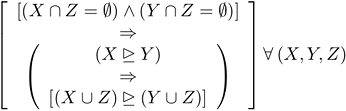 in which X, Y, and Z are sets of events. The underscored arrowhead is again my notation for
in which X, Y, and Z are sets of events. The underscored arrowhead is again my notation for 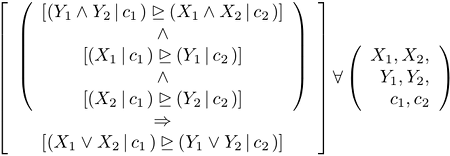 To get di Finetti's principle from it, set
To get di Finetti's principle from it, set 