One of the principles often suggested as an axiom of probability is that of additivity. The additivity here is a generalization of arithmetic addivity — which generalization, with other assumptions, will imply the arithmetic case.

The classic formulation of this principle came from Bruno di Finetti. Di Finetti was a subjectivist. A typical subjectivist is amongst those who prefer to think in terms of the probability of events, rather than in terms of the probability of propositions. And subjectivists like to found their theory of probability in terms of unconditional probabilities. Using somewhat different notation from that here, the classic formulation of the principle of additivity is 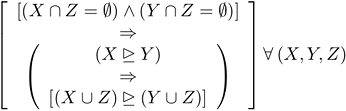in which X, Y, and Z are sets of events. The underscored arrowhead is again my notation for weak supraprobability, the union of strict supraprobability with equiprobability.

One of the things that I noticed when considering this proposition is that the condition that Y∩Z be empty is superfluous. I tried to get a note published on that issue, but journals were not receptive. I had bigger fish to fry other than that one, so I threw-up my hands and moved onward.

When it comes to probability, I'm a logicist. I see probability as primarily about relations amongst propositions (though every event corresponds to a proposition that the event happen and every proposition corresponds to the event that the proposition is true), and I see each thing about which we state a probability as a compound proposition of the form X given c in which X and c are themselves propositions (though if c is a tautology, then the proposition operationalizes as unconditional). I've long pondered what would be a proper generalized restatement of the principle of additivity. If you've looked at the set of axiomata on which I've been working, then you've seen one or more of my efforts. Last night, I clearly saw what I think to be the proper statement: 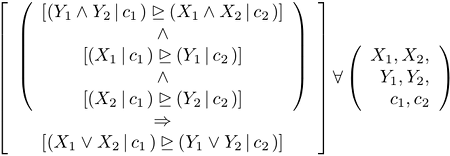To get di Finetti's principle from it, set c₂ = c₁ and make it a tautology, and set X₂ = Z = Y₂. Note that the condition of (X₂ | c₁) being weakly supraprobable to (Y₂ | c₂) is automatically met when the two are the same thing. By itself, this generalization implies my previous generalization and part of another principle that I was treating as an axiom; the remainder of that other principle can be got by applying basic properties of equiprobability and the principle that strict supraprobability and equiprobability are mutually exclusive to this generalization. The principle that is thus demoted was awkward; the axiom that was recast as acceptable as it was, but the new version is elegant.

Tags: papers, plausibility, probability, qualitative probability

This entry was posted and is filed under epistemology, personal, public. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.